指数函数与对数函数知识点总结(指数函数对数函数知识点整理)

指数函数与对数函数知识点总结

指数函数和对数函数是高中数学中的重要内容，它们在数学和科学领域中具有广泛的应用。本文将详细介绍指数函数和对数函数的定义、性质以及它们之间的关系。

指数函数是以一个固定的底数为基础，指数为自变量的函数。通常表示为y = a^x，其中a是底数，x是指数，y是函数值。指数函数的特点是随着指数的增加或减少，函数值呈指数级别的变化。当底数大于1时，指数函数呈增长趋势；当底数在0和1之间时，指数函数呈下降趋势。

对数函数是指数函数的逆运算。通常表示为y = logₐx，其中a是底数，x是函数值，y是指数。对数函数的特点是将一个数转换成另一个数的指数形式。当底数大于1时，对数函数的函数值为正；当底数在0和1之间时，对数函数的函数值为负。

这两个函数之间存在着重要的关系。指数函数和对数函数是互为反函数，即y = a^x 和 x = logₐy 是等价的。这意味着，将一个数进行指数运算后再进行对数运算，结果将回到原来的数值。

指数函数和对数函数在实际应用中非常重要。在金融领域，复利计算就是基于指数函数的原理。在生物学中，指数增长函数可以描述种群的增长规律。在物理学中，放射性衰变过程可以使用指数函数和对数函数来描述。

综上所述，指数函数和对数函数是数学中的重要概念。它们不仅具有丰富的性质和应用，而且在解决实际问题时具有重要的作用。

参考图片：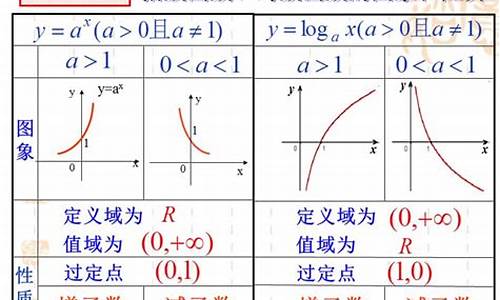

总结归纳

指数函数和对数函数是数学中的重要内容。指数函数以固定底数为基础，指数为自变量，呈指数级别的变化；对数函数是指数函数的逆运算，将一个数转换成另一个数的指数形式。指数函数和对数函数是互为反函数，它们之间的转换可以帮助我们解决各种实际问题。无论是在金融、生物学还是物理学等领域，指数函数和对数函数都发挥着重要的作用。通过深入学习和理解这两个函数，我们能够更好地应用它们解决实际问题，提升数学思维能力。